Karnaugh Map
一、Karnaugh Map
1.1 最小项
最小项的定义:一个函数的某个乘积项包含了函数的全部变量,其中每个变量都以原变量或反变量的形式出现,且仅出现一次,则这个乘积项称为该函数的一个标准积项,通常称为最小项。
最小项的表示方法:通常用\(m_i\)来表示最小项。
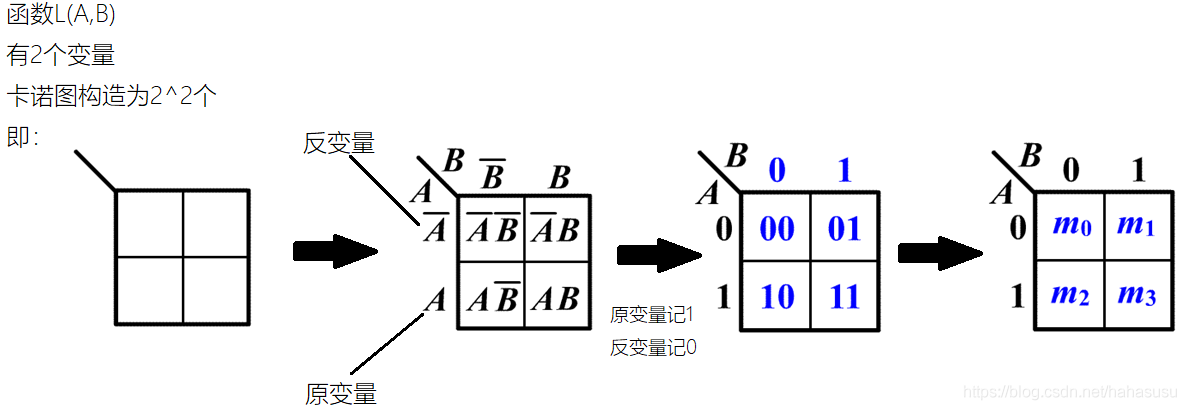
下标i的确定方式:把最小项中原变量记为1,反变量记为0,当变量顺序确定后,可以按顺序排列成一个二进制数,则与这个二进制数相对应的十进制数,就是这个最小项的下标i。
Example:
函数\(L(A,B,C)\)的最小项为:
\[\overline{A}\overline{B}\overline{C}, \overline{A}\overline{B}C, \overline{A}B\overline{C}, \overline{A}BC, A\overline{B}\overline{C}, A\overline{B}C, AB\overline{C}, ABC\]
分别对应:
\[000, 001, 010, 011, 100, 101, 110, 111\]
\(m_i\)的表达方式:
\[m_0, m_1, m_2, m_3, m_4, m_5, m_6, m_7\]
最小项的的相邻性:任何两个最小项如果他们只有一个因子不同,其余因子都相同,则称这两个最小项为相邻最小项。
Example:\(m_0\)和\(m_1\)具有相邻性,\(m_1\)和\(m_2\)却没有,因为他们有两个不同的因子。
相邻的两个最小项之和可以合并一项,消去一个变量。如:
\[m_0 + m_2 = \overline{A}\overline{B}\overline{C} + \overline{A}B\overline{C} = \overline{A}(\overline{B} + B)\overline{C} = \overline{A}\overline{C}\]
1.2 卡诺图
- 一种描述逻辑函数特殊方格图。
- 每格代表一个最小项,上下左右相邻就具备相邻性。
- 有n个变量,最小项就有\(2^n\)且卡诺图也由\(2^n\)个格子构成。
两变量卡诺图:
三变量卡诺图:

逻辑函数\(F(A, B, C, D) = \sum m (0,1,2,5,7,8,10,11,14,15)\)的卡诺图:

1.3 逻辑函数的卡诺图化简法
诺图相邻性的特点保证了几何相邻两方格所代表的最小项只有一个变量不同。因此,若相邻的方格都为1(简称1格)时,则对应的最小项就可以合并。合并的结果是消去这个不同的变量,只保留相同的变量。这是图形化简法的依据。
综上所述,卡诺图具备以下特性:
- 卡诺图中两个相邻1格的最小项可以合并成一个与(加)项,并消去一个变量。
- 卡诺图中四个相邻1格的最小项可以合并成一个与(加)项,并消去两个变量。
- 卡诺图中八个相邻1格的最小项可以合并成一个与(加)项,并消去三个变量。
利用这3点特性来接着看下面的例子:

上图两个相邻1格的最小项可以合并成一个与项,并消去一个变量,化简式子如下:
\[m_1 = m_5 = \overline{A}\overline{B}C + A\overline{B}C = (\overline{A} + A)\overline{B}C = \overline{B}C\]
根据上面3个特性再来看几个例子加深理解,以下是4个相邻1格的: 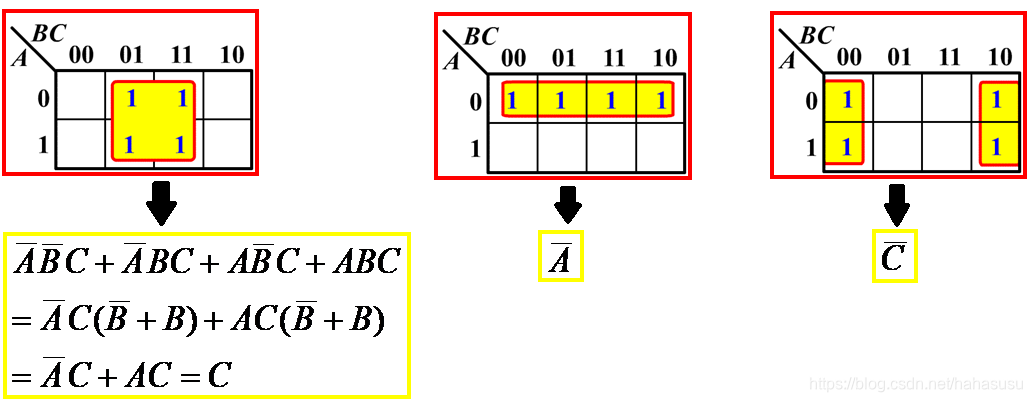
Example:
\[F(A,B,C) = \sum(1,2,3,6,7)\]
先画出卡诺图,然后转换十进制对应1,2,3,6,7的地方填入为1,其余填写为0(这个步骤有前面的知识点支撑,应该不难理解了。)

然后获得式子:\(F = (m_1 + m_3) + (m_2 + m_3 + m_6 + m_7)\)
即:
\[F = \overline{A}C + B\]
首先,有这么几点需要明确:
- 列出逻辑函数的最小项表达式,由最小项表达式确定变量的个数(如果最小项中缺少变量,应按例的方法补齐)。
- 画出最小项表达式对应的卡诺图。
- 将卡诺图中的1格画圈,一个也不能漏圈,否则最后得到的表达式就会与所给函数不等;1格允许被一个以上的圈所包围。
- 圈的个数应尽可能得少。即在保证1格一个也不漏圈的前提下,圈的个数越少越好。因为一个圈和一个与项相对应,圈数越少,与或表达式的与项就越少。
- 按照2k个方格来组合(即圈内的1格数必须为1,2,4,8等),圈的面积越大越好。因为圈越大,可消去的变量就越多,与项中的变量就越少。
- 每个圈应至少包含一个新的1格,否则这个圈是多余的。
- 用卡诺图化简所得到的最简与或式不是唯一的。